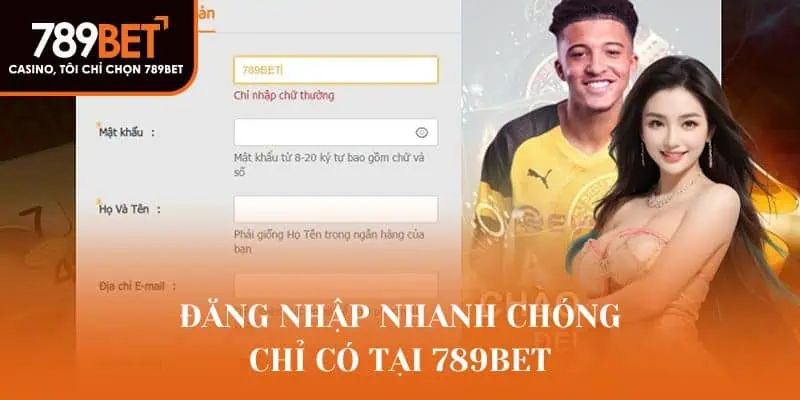
Dưới đây là hướng dẫn chi tiết 5 bước đơn giản để đăng ký tài khoản tại nhà cái, giúp bạn nhanh chóng tham gia và trải nghiệm những tựa game thú vị trên nền tảng này.
- Bước 1: Truy cập vào website chính thức của 789Bet bằng trình duyệt trên máy tính hoặc điện thoại. Tại giao diện chính, tìm và nhấn vào nút “Đăng ký” nằm ở góc trên cùng bên phải màn hình để bắt đầu quá trình tạo tài khoản.
- Bước 2: Người chơi nhập đầy đủ các thông tin cần thiết như tên đăng nhập, mật khẩu, email, số điện thoại và mã xác nhận. Hãy đảm bảo mọi thông tin cung cấp chính xác để tránh gặp khó khăn khi xác minh hoặc rút tiền sau này.
- Bước 3: Nhập lại mật khẩu để đảm bảo tính chính xác. Kiểm tra toàn bộ thông tin vừa điền một cách cẩn thận. Đây là bước quan trọng giúp tài khoản của bạn được tạo thành công và tránh xảy ra sai sót không đáng có.
- Bước 4: Tích chọn vào ô “Đồng ý với điều khoản và điều kiện” mà nhà cái 789Bet đưa ra. Sau đó, nhấn vào nút “Đăng ký” để hoàn tất quá trình.